Prove That Continuous Function Must Be Bounded

A mathematical function the set of whose values is bounded

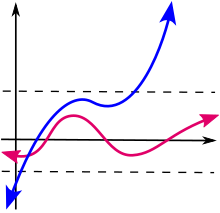
A schematic illustration of a bounded function (red) and an unbounded one (blue). Intuitively, the graph of a bounded function stays within a horizontal band, while the graph of an unbounded function does not.

In mathematics, a function f defined on some set X with real or complex values is called bounded if the set of its values is bounded. In other words, there exists a real number M such that

${\displaystyle |f(x)|\leq M}$

for all x in X.^[1] A function that is not bounded is said to be unbounded.^{[ citation needed ]}

If f is real-valued and f(x) ≤ A for all x in X, then the function is said to be bounded (from) above by A. If f(x) ≥ B for all x in X, then the function is said to be bounded (from) below by B. A real-valued function is bounded if and only if it is bounded from above and below.^{[1] [ additional citation(s) needed ]}

An important special case is a bounded sequence, where X is taken to be the set N of natural numbers. Thus a sequence f = (a ₀, a ₁, a ₂, ...) is bounded if there exists a real number M such that

${\displaystyle |a_{n}|\leq M}$

for every natural number n. The set of all bounded sequences forms the sequence space ${\displaystyle l^{\infty }}$ .^{[ citation needed ]}

The definition of boundedness can be generalized to functions f : X → Y taking values in a more general space Y by requiring that the image f(X) is a bounded set in Y.^{[ citation needed ]}

[edit]

Weaker than boundedness is local boundedness. A family of bounded functions may be uniformly bounded.

A bounded operator T : X → Y is not a bounded function in the sense of this page's definition (unless T = 0), but has the weaker property of preserving boundedness: Bounded sets M ⊆ X are mapped to bounded sets T(M) ⊆ Y. This definition can be extended to any function f : X → Y if X and Y allow for the concept of a bounded set. Boundedness can also be determined by looking at a graph.^{[ citation needed ]}

Examples [edit]

• The sine function sin : R → R is bounded since ${\displaystyle |\sin(x)|\leq 1}$ for all ${\displaystyle x\in \mathbf {R} }$ .^{[1] [2]}
• The function ${\displaystyle f(x)=(x^{2}-1)^{-1}}$ , defined for all real x except for −1 and 1, is unbounded. As x approaches −1 or 1, the values of this function get larger in magnitude. This function can be made bounded if one restricts its domain to be, for example, [2, ∞) or (−∞, −2].^{[ citation needed ]}
• The function ${\textstyle f(x)=(x^{2}+1)^{-1}}$ , defined for all real x, is bounded, since ${\textstyle |f(x)|\leq 1}$ for all x.^{[ citation needed ]}
• The inverse trigonometric function arctangent defined as: y = arctan(x) or x = tan(y) is increasing for all real numbers x and bounded with − π / 2 < y < π / 2 radians^[3]
• By the boundedness theorem, every continuous function on a closed interval, such as f : [0, 1] → R, is bounded.^[4] More generally, any continuous function from a compact space into a metric space is bounded.^{[ citation needed ]}
• All complex-valued functions f : C → C which are entire are either unbounded or constant as a consequence of Liouville's theorem.^[5] In particular, the complex sin : C → C must be unbounded since it is entire.^{[ citation needed ]}
• The function f which takes the value 0 for x rational number and 1 for x irrational number (cf. Dirichlet function) is bounded. Thus, a function does not need to be "nice" in order to be bounded. The set of all bounded functions defined on [0, 1] is much larger than the set of continuous functions on that interval.^{[ citation needed ]} Moreover, continuous functions need not be bounded; for example, the functions ${\displaystyle g:\mathbb {R} ^{2}\to \mathbb {R} }$ and ${\displaystyle h:(0,1)^{2}\to \mathbb {R} }$ defined by ${\displaystyle g(x,y):=x+y}$ and ${\displaystyle h(x,y):={\frac {1}{x+y}}}$ are both continuous, but neither is bounded.^[6] (However, a continuous function must be bounded if its domain is both closed and bounded.^[6])

References [edit]

1. ^ ^{a b c} Jeffrey, Alan (1996-06-13). Mathematics for Engineers and Scientists, 5th Edition. CRC Press. ISBN978-0-412-62150-5.
2. ^ "The Sine and Cosine Functions" (PDF). math.dartmouth.edu. Archived (PDF) from the original on 2 February 2013. Retrieved 1 September 2021.
3. ^ Polyanin, Andrei D.; Chernoutsan, Alexei (2010-10-18). A Concise Handbook of Mathematics, Physics, and Engineering Sciences. CRC Press. ISBN978-1-4398-0640-1.
4. ^ Weisstein, Eric W. "Extreme Value Theorem". mathworld.wolfram.com . Retrieved 2021-09-01 .
5. ^ "Liouville theorems - Encyclopedia of Mathematics". encyclopediaofmath.org . Retrieved 2021-09-01 .
6. ^ ^{a b} Ghorpade, Sudhir R.; Limaye, Balmohan V. (2010-03-20). A Course in Multivariable Calculus and Analysis. Springer Science & Business Media. p. 56. ISBN978-1-4419-1621-1.

See also [edit]

• Bounded set
• Compact support
• Local boundedness
• Uniform boundedness

brackettthatten.blogspot.com

Source: https://en.wikipedia.org/wiki/Bounded_function

Share this post